Évariste Galois
From Wikipedia, the free encyclopedia
"Galois" redirects here. For other uses, see Gallois (disambiguation).
| Évariste Galois | |
|---|---|
 |
|
| Born | October 25, 1811 Bourg-la-Reine, French Empire |
| Died | May 31, 1832 (aged 20) Paris, Kingdom of France |
| Nationality | |
| Fields | Mathematics |
| Known for | Work on the theory of equations and Abelian integrals |
| Signature |
|
Life
Early life
Galois was born on October 25, 1811, to Nicolas-Gabriel Galois and Adélaïde-Marie (born Demante). His father was a Republican and was head of Bourg-la-Reine's liberal party. He became mayor of the village after Louis XVIII returned to the throne in 1814. His mother, the daughter of a jurist, was a fluent reader of Latin and classical literature and was responsible for her son's education for his first twelve years. At the age of 10, Galois was offered a place at the college of Reims, but his mother preferred to keep him at home.In October 1823, he entered the Lycée Louis-le-Grand, and despite some turmoil in the school at the beginning of the term (when about a hundred students were expelled), Galois managed to perform well for the first two years, obtaining the first prize in Latin. He soon became bored with his studies, and at the age of 14, began to take a serious interest in mathematics.
He found a copy of Adrien Marie Legendre's Éléments de Géométrie, which it is said that he read "like a novel" and mastered at the first reading. At 15, he was reading the original papers of Joseph Louis Lagrange, such as the landmark Réflexions sur la résolution algébrique des équations which likely motivated his later work on equation theory, and Leçons sur le calcul des fonctions, work intended for professional mathematicians. Yet his classwork remained uninspired, and his teachers accused him of affecting ambition and originality in a negative way.[2]
In 1828, he attempted the entrance exam to École Polytechnique, the most prestigious institution for mathematics in France at the time, without the usual preparation in mathematics, and failed for lack of explanations on the oral examination. In that same year, he entered the École Normale (then known as l'École préparatoire), a far inferior institution for mathematical studies at that time, where he found some professors sympathetic to him.
In the following year, Galois' first paper, on continued fractions,[3] was published. It was at around the same time that he began making fundamental discoveries in the theory of polynomial equations. He submitted two papers on this topic to the Academy of Sciences. Augustin Louis Cauchy refereed these papers, but refused to accept them for publication for reasons that still remain unclear. However, in spite of many claims to the contrary, it appears that Cauchy recognized the importance of Galois' work, and that he merely suggested combining the two papers into one in order to enter it in the competition for the Academy's Grand Prize in Mathematics. Cauchy, a highly eminent mathematician of the time, considered Galois' work to be a likely winner.[4]
On July 28, 1829, Galois' father committed suicide after a bitter political dispute with the village priest. A couple of days later, Galois made his second and last attempt at entering the Polytechnique, and failed yet again. It is undisputed that Galois was more than qualified; however, accounts differ on why he failed. The legend holds that he thought the exercise proposed to him by the examiner to be of no interest, and, in exasperation, threw at the examiner's head the rag used to erase the blackboard.[5][6] More plausible accounts state that Galois made too many logical leaps and baffled the incompetent examiner, evoking the student's rage. The recent death of his father may have also influenced his behavior.[2]
Having been denied admission to the Polytechnique, Galois took the Baccalaureate examinations in order to enter the École Normale. He passed, receiving his degree on December 29, 1829. His examiner in mathematics reported, "This pupil is sometimes obscure in expressing his ideas, but he is intelligent and shows a remarkable spirit of research."
He submitted his memoir on equation theory several times, but it was never published in his lifetime due to various events. As noted before, his first attempt was refused by Cauchy, but he tried again in February 1830 after following Cauchy's suggestions and submitted it to the Academy's secretary Fourier, to be considered for the Grand Prix of the Academy. Unfortunately, Fourier died soon after, and the memoir was lost. The prize would be awarded that year to Abel posthumously and also to Jacobi. Despite the lost memoir, Galois published three papers that year, one laid the foundations for Galois theory,[7] the second one about the numerical resolution of equations (root finding in modern terminology),[8] and the third, an important one on number theory, where the concept of a finite field was first articulated.[9]
Political firebrand
Galois lived during a time of political turmoil in France. Charles X had succeeded Louis XVIII in 1824, but in 1827 his party suffered a major electoral setback and by 1830 the opposition liberal party became the majority. Charles, faced with abdication, staged a coup d'état, and issued his notorious July Ordinances, touching off the July Revolution which ended with Louis-Philippe becoming king. While their counterparts at Polytechnique were making history in the streets during les Trois Glorieuses, Galois and all the other students at the École Normale were locked in by the school's director. Galois was incensed and wrote a blistering letter criticizing the director, which he submitted to the Gazette des Écoles, signing the letter with his full name. Although the Gazette's editor redacted the signature for publication, Galois was expelled.[6]Although his expulsion would have formally taken effect on January 4, 1831, Galois quit school immediately and joined the staunchly Republican artillery unit of the National Guard. These and other political affiliations continually distracted him from mathematical work. Due to controversy surrounding the unit, soon after Galois became a member, on December 31, 1830, the artillery of the National Guard was disbanded out of fear that they might destabilize the government. At around the same time, nineteen officers of Galois' former unit were arrested and charged with conspiracy to overthrow the government.
In April, the officers were acquitted of all charges, and on May 9, 1831, a banquet was held in their honor, with many illustrious people present, such as Alexandre Dumas. The proceedings grew riotous, and Galois proposed a toast to King Louis-Philippe with a dagger above his cup, which was interpreted as a threat against the king's life. He was arrested the following day, but was acquitted on June 15.[6][10]
On the following Bastille Day, Galois was at the head of a protest, wearing the uniform of the disbanded artillery, and came heavily armed with several pistols, a rifle, and a dagger. For this, he was again arrested and this time was sentenced to six months in prison for illegally wearing a uniform.[5] He was released on April 29, 1832. During his imprisonment, he continued developing his mathematical ideas.
Final days

The Galois memorial in the cemetery of Bourg-la-Reine. Évariste Galois was buried in a common grave and the exact location is still unknown.
Galois' fatal duel took place on May 30. The true motives behind the duel will most likely remain forever obscure. There has been much speculation, much of it spurious, as to the reasons behind it. What is known is that five days before his death, he wrote a letter to Chevalier which clearly alludes to a broken love affair.[4]
Some archival investigation on the original letters suggests that the woman of romantic interest was a Mademoiselle Stéphanie-Félicie Poterin du Motel, the daughter of the physician at the hostel where Galois stayed during the last months of his life. Fragments of letters from her copied by Galois himself (with many portions either obliterated, such as her name, or deliberately omitted) are available.[12] The letters hint that Mlle. du Motel had confided some of her troubles with Galois, and this might have prompted him to provoke the duel himself on her behalf. This conjecture is also supported by other letters Galois later wrote to his friends the night before he died. Much more detailed speculation based on these scant historical details has been interpolated by many of Galois' biographers (most notably by Eric Temple Bell in Men of Mathematics), such as the frequently repeated speculation that the entire incident was stage-managed by the police and royalist factions to eliminate a political enemy.[5]
As to his opponent in the duel, Alexandre Dumas names Pescheux d'Herbinville, one of the nineteen artillery officers whose acquittal was celebrated at the banquet that occasioned Galois' first arrest[10] and du Motel's fiancé.[citation needed] However, Dumas is alone in this assertion, and extant newspaper clippings from only a few days after the duel give a description of his opponent that more accurately applies to one of Galois' Republican friends, most probably Ernest Duchatelet, who was imprisoned with Galois on the same charges. Given the conflicting information available, the true identity of his killer may well be lost to history.
Whatever the reasons behind the duel, Galois was so convinced of his impending death that he stayed up all night writing letters to his Republican friends and composing what would become his mathematical testament, the famous letter to Auguste Chevalier outlining his ideas, and three attached manuscripts.[13] Hermann Weyl, a mathematician, said of this testament, "This letter, if judged by the novelty and profundity of ideas it contains, is perhaps the most substantial piece of writing in the whole literature of mankind." However, the legend of Galois pouring his mathematical thoughts onto paper the night before he died seems to have been exaggerated. In these final papers, he outlined the rough edges of some work he had been doing in analysis and annotated a copy of the manuscript submitted to the Academy and other papers.
Early in the morning of May 30, 1832, he was shot in the abdomen and died the following day at ten in the Cochin hospital (probably of peritonitis) after refusing the offices of a priest. He was 20 years old. His last words to his brother Alfred were:
Ne pleure pas, Alfred ! J'ai besoin de tout mon courage pour mourir à vingt ans ! (Don't cry, Alfred! I need all my courage to die at twenty.)On June 2, Évariste Galois was buried in a common grave of the Montparnasse cemetery whose exact location is unknown.[14] In the cemetery of his native town - Bourg-la-Reine - a cenotaph in his honour was erected beside the graves of his relatives.[15]
Galois' mathematical contributions were published in full in 1843 when Liouville reviewed his manuscript and declared it sound. It was finally published in the October–November 1846 issue of the Journal de Mathématiques Pures et Appliquées.[16] The most famous contribution of this manuscript was a novel proof that there is no quintic formula, that is, that fifth and higher degree equations are not solvable by radicals. Although Abel had already proved the impossibility of a "quintic formula" by radicals in 1824 and Ruffini had published a solution in 1799 that turned out to be flawed, Galois' methods led to deeper research in what is now called Galois theory. For example, one can use it to determine, for any polynomial equation, whether it has a solution by radicals.
[edit] Contributions to mathematics
Unsurprisingly, Galois' collected works amount to only some 60 pages, but within them are many important ideas that have had far-reaching consequences for nearly all branches of mathematics.[17] His work has been compared to that of Niels Henrik Abel, another mathematician who died at a very young age, and much of their work had significant overlap.Tu prieras publiquement Jacobi ou Gauss de donner leur avis, non sur la vérité, mais sur l'importance des théorèmes. Après cela, il y aura, j'espère, des gens qui trouveront leur profit à déchiffrer tout ce gâchis.
(Ask Jacobi or Gauss publicly to give their opinion, not as to the truth, but as to the importance of these theorems. Later there will be, I hope, some people who will find it to their advantage to decipher all this mess.)
[edit] Algebra
While many mathematicians before Galois gave consideration to what are now known as groups, it was Galois who was the first to use the word group (in French groupe) in a sense close to the technical sense that is understood today, making him among the founders of the branch of algebra known as group theory. He developed the concept that is today known as a normal subgroup. He called the decomposition of a group into its left and right cosets a proper decomposition if the left and right cosets coincide, which is what today is known as a normal subgroup.[13] He also introduced the concept of a finite field (also known as a Galois field in his honor), in essentially the same form as it is understood today.[9]In his last letter to Chevalier[13] and attached manuscripts, the second of three, he made basic studies of linear groups over finite fields:
- He constructed the general linear group over a prime field, GL(ν, p) and computed its order, in studying the Galois group of the general equation of degree pν.[18]
- He constructed the projective special linear group PSL(2,p). Galois constructed them as fractional linear transforms, and observed that they were simple except if p was 2 or 3.[19] These were the second family of finite simple groups, after the alternating groups.[20]
- He noted the exceptional fact that PSL(2,p) is simple and acts on p points if and only if p is 5, 7, or 11.[21][22]
[edit] Galois theory
Main article: Galois theory
Galois' most significant contribution to mathematics by far is his
development of Galois theory. He realized that the algebraic solution to
a polynomial equation is related to the structure of a group of permutations associated with the roots of the polynomial, the Galois group of the polynomial. He found that an equation could be solved in radicals if one can find a series of subgroups of its Galois group, each one normal in its successor with abelian quotient, or its Galois group is solvable. This proved to be a fertile approach, which later mathematicians adapted to many other fields of mathematics besides the theory of equations to which Galois originally applied it.[17][edit] Analysis
| This section requires expansion. |
[edit] See also
[edit] Notes
- ^ Stewart, J., et al. Algebra and Trigonometry. p. 334.
- ^ a b c Stewart, Ian (1973). Galois Theory. London: Chapman and Hall. pp. xvii-xxii. ISBN 0412108003.
- ^ Galois, Évariste (1828). "Démonstration d'un théorème sur les fractions continues périodiques". Annales de Mathématiques XIX: 294.
- ^ a b c Rothman, Tony. "Genius and Biographers: The Fictionalization of Evariste Galois". Retrieved 2009-02-04.
- ^ a b c Bell, Eric Temple (1986). Men of Mathematics. New York: Simon and Schuster. ISBN 0-671-62818-6.
- ^ a b c d Dupuy, Paul. "La vie d'Évariste Galois". Annales de l'École Normale 13: 197–266.
- ^ Galois, Évariste (1830). "Analyse d'un Mémoire sur la résolution algébrique des équations". Bulletin des Sciences mathématiques XIII: 271.
- ^ Galois, Évariste (1830). "Note sur la résolution des équations numériques". Bulletin des Sciences mathématiques XIII: 413.
- ^ a b Galois, Évariste (1830). "Sur la théorie des nombres". Bulletin des Sciences mathématiques XIII: 428.
- ^ a b Dumas (père), Alexandre. "CCIV". Mes Mémoires. ISBN 1437155952. Retrieved 2010-04-13.
- ^ Taton, R. (1947). "Les relations d'Évariste Galois avec les mathématiciens de son temps". Revue d'histoire des sciences et de leurs applications 1 (2): 114. doi:10.3406/rhs.1947.2607.
- ^ Bourgne, R.; J.-P. Azra (1962). Écrits et mémoires mathématiques d'Évariste Galois. Paris: Gauthier-Villars.
- ^ a b c Galois, Évariste (1846). "Lettre de Galois à M. Auguste Chevalier". Journal des mathématiques pures et appliquées XI: 408–415. Retrieved 2009-02-04.
- ^ Escofier, Jean-Pierre (2001). Galois Theory. Springer. pp. 224. ISBN 0387987657.
- ^ Rigatelli, Laura Toti (1996). Evariste Galois, 1811–1832 (Vita mathematica, 11). Birkhäuser. pp. 114. ISBN 3764354100.
- ^ Galois, Évariste (1846). "OEuvres mathématiques d'Évariste Galois.". Journal des mathématiques pures et appliquées XI: 381–444. Retrieved 2009-02-04.
- ^ a b Lie, Sophus (1895). "Influence de Galois sur le Développement des Mathématiques". Le centenaire de l'École Normale 1795–1985. Hachette.
- ^ Letter, p. 410
- ^ Letter, p. 411
- ^ Wilson, Robert A. (2009). "Chapter 1: Introduction". The finite simple groups. Graduate Texts in Mathematics 251. 251. Berlin, New York: Springer-Verlag. doi:10.1007/978-1-84800-988-2. ISBN 978-1-84800-987-5. Zbl 05622792, 2007 preprint
- ^ Letter, pp. 411–412
- ^ Galois' last letter, Never Ending Books
Srinivasa Ramanujan
From Wikipedia, the free encyclopedia
"Ramanujan" redirects here. For other uses, see Ramanujan (disambiguation).
| Srinivasa Ramanujan | |
|---|---|
 |
|
| Born | 22 December 1887 Erode, Madras, India |
| Died | 26 April 1920 (aged 32) Chetput, (Madras), India |
| Residence | India |
| Nationality | Indian |
| Fields | Mathematics |
| Alma mater | Government Arts College Pachaiyappa's College The University of Cambridge |
| Academic advisors | G. H. Hardy J. E. Littlewood |
| Known for | Landau–Ramanujan constant Mock theta functions Ramanujan conjecture Ramanujan prime Ramanujan–Soldner constant Ramanujan theta function Ramanujan's sum Rogers–Ramanujan identities |
| Influences | G. H. Hardy |
Born in Erode, Tamil Nadu, India, to a poor Brahmin family, Ramanujan first encountered formal mathematics at age 10. He demonstrated a natural ability, and was given books on advanced trigonometry written by S. L. Loney.[2] He mastered them by age 12, and even discovered theorems of his own, including independently re-discovering Euler's identity. He demonstrated unusual mathematical skills at school, winning accolades and awards. By 17, Ramanujan conducted his own mathematical research on Bernoulli numbers and the Euler–Mascheroni constant. He received a scholarship to study at Government College in Kumbakonam, but lost it when he failed his non-mathematical coursework. He joined another college to pursue independent mathematical research, working as a clerk in the Accountant-General's office at the Madras Port Trust Office to support himself.[3] In 1912–1913, he sent samples of his theorems to three academics at the University of Cambridge. Only Hardy recognised the brilliance of his work, subsequently inviting Ramanujan to visit and work with him at Cambridge. He became a Fellow of the Royal Society and a Fellow of Trinity College, Cambridge, dying of illness, malnutrition and possibly liver infection in 1920 at the age of 32.
During his short lifetime, Ramanujan independently compiled nearly 3900 results (mostly identities and equations).[4] Although a small number of these results were actually false and some were already known, most of his claims have now been proven correct.[5] He stated results that were both original and highly unconventional, such as the Ramanujan prime and the Ramanujan theta function, and these have inspired a vast amount of further research.[6] However, the mathematical mainstream has been rather slow in absorbing some of his major discoveries. The Ramanujan Journal, an international publication, was launched to publish work in all areas of mathematics influenced by his work.[7]
Early life
Ramanujan was born on 22 December 1887 in the city Erode, Tamil Nadu, India, at the residence of his maternal grandparents.[8] His father, K. Srinivasa Iyengar worked as a clerk in a sari shop and hailed from the district of Thanjavur.[9] His mother, Komalatammal was a housewife and also sang at a local temple.[10] They lived in Sarangapani Street in a traditional home in the town of Kumbakonam. The family home is now a museum. When Ramanujan was a year and a half old, his mother gave birth to a son named Sadagopan, who died less than three months later. In December 1889, Ramanujan had smallpox and recovered, unlike thousands in the Thanjavur district who died from the disease that year.[11] He moved with his mother to her parents' house in Kanchipuram, near Madras (now Chennai). In November 1891, and again in 1894, his mother gave birth, but both children died in infancy.On 1 October 1892, Ramanujan was enrolled at the local school.[12] In March 1894, he was moved to a Telugu medium school. After his maternal grandfather lost his job as a court official in Kanchipuram,[13] Ramanujan and his mother moved back to Kumbakonam and he was enrolled in the Kangayan Primary School.[14] After his paternal grandfather died, he was sent back to his maternal grandparents, who were now living in Madras. He did not like school in Madras, and he tried to avoid attending. His family enlisted a local constable to make sure he attended school. Within six months, Ramanujan was back in Kumbakonam.[14]
Since Ramanujan's father was at work most of the day, his mother took care of him as a child. He had a close relationship with her. From her, he learned about tradition and puranas. He learned to sing religious songs, to attend pujas at the temple and particular eating habits – all of which are part of Brahmin culture.[15] At the Kangayan Primary School, Ramanujan performed well. Just before the age of 10, in November 1897, he passed his primary examinations in English, Tamil, geography and arithmetic. With his scores, he finished first in the district.[16] That year, Ramanujan entered Town Higher Secondary School where he encountered formal mathematics for the first time.[16]
By age 11, he had exhausted the mathematical knowledge of two college students who were lodgers at his home. He was later lent a book on advanced trigonometry written by S. L. Loney.[17][18] He completely mastered this book by the age of 13 and discovered sophisticated theorems on his own. By 14, he was receiving merit certificates and academic awards which continued throughout his school career and also assisted the school in the logistics of assigning its 1200 students (each with their own needs) to its 35-odd teachers.[19] He completed mathematical exams in half the allotted time, and showed a familiarity with infinite series. In 1903 when he was 16, Ramanujan obtained a library loaned copy of a book by G. S. Carr from a friend.[20][21] The book was titled A Synopsis of Elementary Results in Pure and Applied Mathematics and was a collection of 5000 theorems. Ramanujan reportedly studied the contents of the book in detail.[22] The book is generally acknowledged as a key element in awakening the genius of Ramanujan.[22] The next year, he had independently developed and investigated the Bernoulli numbers and had calculated Euler's constant up to 15 decimal places.[23] His peers at the time commented that they "rarely understood him" and "stood in respectful awe" of him.[19]
When he graduated from Town Higher Secondary School in 1904, Ramanujan was awarded the K. Ranganatha Rao prize for mathematics by the school's headmaster, Krishnaswami Iyer. Iyer introduced Ramanujan as an outstanding student who deserved scores higher than the maximum possible marks.[19] He received a scholarship to study at Government Arts College, Kumbakonam,[24][25] However, Ramanujan was so intent on studying mathematics that he could not focus on any other subjects and failed most of them, losing his scholarship in the process.[26] In August 1905, he ran away from home, heading towards Visakhapatnam.[27] He later enrolled at Pachaiyappa's College in Madras. He again excelled in mathematics but performed poorly in other subjects such as physiology. Ramanujan failed his Fine Arts degree exam in December 1906 and again a year later. Without a degree, he left college and continued to pursue independent research in mathematics. At this point in his life, he lived in extreme poverty and was often on the brink of starvation.[28]
Adulthood in India
On 14 July 1909, Ramanujan was married to a nine-year old bride, Janaki Ammal.[29] In the branch of Hinduism to which Ramanujan belonged, marriage was a formal engagement that was consummated only after the bride turned 17 or 18, as per the traditional calendar.After the marriage, Ramanujan developed a hydrocele testis, an abnormal swelling of the tunica vaginalis, an internal membrane in the testicle.[30] The condition could be treated with a routine surgical operation that would release the blocked fluid in the scrotal sac. His family did not have the money for the operation, but in January 1910, a doctor volunteered to do the surgery for free.[31]
After his successful surgery, Ramanujan searched for a job. He stayed at friends' houses while he went door to door around the city of Madras (now Chennai) looking for a clerical position. To make some money, he tutored some students at Presidency College who were preparing for their F.A. exam.[32]
In late 1910, Ramanujan was sick again, possibly as a result of the surgery earlier in the year. He feared for his health, and even told his friend, R. Radakrishna Iyer, to "hand these [my mathematical notebooks] over to Professor Singaravelu Mudaliar [mathematics professor at Pachaiyappa's College] or to the British professor Edward B. Ross, of the Madras Christian College."[33] After Ramanujan recovered and got back his notebooks from Iyer, he took a northbound train from Kumbakonam to Villupuram, a coastal city under French control.[34][35]
Attention from mathematicians
He met deputy collector V. Ramaswamy Aiyer, who had recently founded the Indian Mathematical Society.[36] Ramanujan, wishing for a job at the revenue department where Ramaswamy Aiyer worked, showed him his mathematics notebooks. As Ramaswamy Aiyer later recalled:I was struck by the extraordinary mathematical results contained in it [the notebooks]. I had no mind to smother his genius by an appointment in the lowest rungs of the revenue department.[37]Ramaswamy Aiyer sent Ramanujan, with letters of introduction, to his mathematician friends in Madras.[36] Some of these friends looked at his work and gave him letters of introduction to R. Ramachandra Rao, the district collector for Nellore and the secretary of the Indian Mathematical Society.[38][39][40] Ramachandra Rao was impressed by Ramanujan's research but doubted that it was actually his own work. Ramanujan mentioned a correspondence he had with Professor Saldhana, a notable Bombay mathematician, in which Saldhana expressed a lack of understanding for his work but concluded that he was not a phony.[41] Ramanujan's friend, C. V. Rajagopalachari, persisted with Ramachandra Rao and tried to quell any doubts over Ramanujan's academic integrity. Rao agreed to give him another chance, and he listened as Ramanujan discussed elliptic integrals, hypergeometric series, and his theory of divergent series, which Rao said ultimately "converted" him to a belief in Ramanujan's mathematical brilliance.[41] When Rao asked him what he wanted, Ramanujan replied that he needed some work and financial support. Rao consented and sent him to Madras. He continued his mathematical research with Rao's financial aid taking care of his daily needs. Ramanujan, with the help of Ramaswamy Aiyer, had his work published in the Journal of Indian Mathematical Society.[42]
One of the first problems he posed in the journal was:
It will be observed that if n is even but not equal to zero,
(i) Bn is a fraction and the numerator of
 in its lowest terms is a prime number,
in its lowest terms is a prime number,(ii) the denominator of Bn contains each of the factors 2 and 3 once and only once,
(iii)
 is an integer and
is an integer and  consequently is an odd integer.
consequently is an odd integer.In his 17-page paper, "Some Properties of Bernoulli's Numbers", Ramanujan gave three proofs, two corollaries and three conjectures.[44] Ramanujan's writing initially had many flaws. As Journal editor M. T. Narayana Iyengar noted:
Mr. Ramanujan's methods were so terse and novel and his presentation so lacking in clearness and precision, that the ordinary [mathematical reader], unaccustomed to such intellectual gymnastics, could hardly follow him.[45]Ramanujan later wrote another paper and also continued to provide problems in the Journal.[46] In early 1912, he got a temporary job in the Madras Accountant General's office, with a salary of 20 rupees per month. He lasted for only a few weeks.[47] Toward the end of that assignment he applied for a position under the Chief Accountant of the Madras Port Trust. In a letter dated 9 February 1912, Ramanujan wrote:
Sir,Attached to his application was a recommendation from E. W. Middlemast, a mathematics professor at the Presidency College, who wrote that Ramanujan was "a young man of quite exceptional capacity in Mathematics".[49] Three weeks after he had applied, on 1 March, Ramanujan learned that he had been accepted as a Class III, Grade IV accounting clerk, making 30 rupees per month.[50] At his office, Ramanujan easily and quickly completed the work he was given, so he spent his spare time doing mathematical research. Ramanujan's boss, Sir Francis Spring, and S. Narayana Iyer, a colleague who was also treasurer of the Indian Mathematical Society, encouraged Ramanujan in his mathematical pursuits.
I understand there is a clerkship vacant in your office, and I beg to apply for the same. I have passed the Matriculation Examination and studied up to the F.A. but was prevented from pursuing my studies further owing to several untoward circumstances. I have, however, been devoting all my time to Mathematics and developing the subject. I can say I am quite confident I can do justice to my work if I am appointed to the post. I therefore beg to request that you will be good enough to confer the appointment on me.[48]
Contacting English mathematicians
On the spring of 1913, Narayana Iyer, Ramachandra Rao and E. W. Middlemast tried to present Ramanujan's work to British mathematicians. One mathematician, M. J. M. Hill of University College London, commented that Ramanujan's papers were riddled with holes.[51] He said that although Ramanujan had "a taste for mathematics, and some ability", he lacked the educational background and foundation needed to be accepted by mathematicians.[52] Although Hill did not offer to take Ramanujan on as a student, he did give thorough and serious professional advice on his work. With the help of friends, Ramanujan drafted letters to leading mathematicians at Cambridge University.[53]The first two professors, H. F. Baker and E. W. Hobson, returned Ramanujan's papers without comment.[54] On 16 January 1913, Ramanujan wrote to G. H. Hardy. Coming from an unknown mathematician, the nine pages of mathematical wonder made Hardy initially view Ramanujan's manuscripts as a possible "fraud".[55] Hardy recognised some of Ramanujan's formulae but others "seemed scarcely possible to believe".[56] One of the theorems Hardy found so incredible was found on the bottom of page three (valid for 0 < a < b + 1/2):
On 8 February 1913, Hardy wrote a letter to Ramanujan, expressing his interest for his work. Hardy also added that it was "essential that I should see proofs of some of your assertions".[61] Before his letter arrived in Madras during the third week of February, Hardy contacted the Indian Office to plan for Ramanujan's trip to Cambridge. Secretary Arthur Davies of the Advisory Committee for Indian Students met with Ramanujan to discuss the overseas trip.[62] In accordance with his Brahmin upbringing, Ramanujan refused to leave his country to "go to a foreign land".[63] Meanwhile, Ramanujan sent a letter packed with theorems to Hardy, writing, "I have found a friend in you who views my labour sympathetically."[64]
To supplement Hardy's endorsement, a former mathematical lecturer at Trinity College, Cambridge, Gilbert Walker, looked at Ramanujan's work and expressed amazement, urging him to spend time at Cambridge.[65] As a result of Walker's endorsement, B. Hanumantha Rao, a mathematics professor at an engineering college, invited Ramanujan's colleague Narayana Iyer to a meeting of the Board of Studies in Mathematics to discuss "what we can do for S. Ramanujan".[66] The board agreed to grant Ramanujan a research scholarship of 75 rupees per month for the next two years at the University of Madras.[67] While he was engaged as a research student, Ramanujan continued to submit papers to the Journal of the Indian Mathematical Society. In one instance, Narayana Iyer submitted some theorems of Ramanujan on summation of series to the above mathematical journal adding “The following theorem is due to S. Ramanujan, the mathematics student of Madras University”. Later in November, British Professor Edward B. Ross of Madras Christian College, whom Ramanujan had met few years ago, stormed into his class one day with his eyes glowing, asking his students, “Does Ramanujan know Polish?” The reason was that in one paper, Ramanujan had anticipated the work of a Polish mathematician whose paper had just arrived by the day’s mail.[68] In his quarterly papers, Ramanujan drew up theorems to make definite integrals more easily solvable. Working off Giuliano Frullani's 1821 integral theorem, Ramanujan formulated generalisations that could be made to evaluate formerly unyielding integrals.[69]
Hardy's correspondence with Ramanujan soured after Ramanujan refused to come to England. Hardy enlisted a colleague lecturing in Madras, E. H. Neville, to mentor and bring Ramanujan to England.[70] Neville asked Ramanujan why he would not go to Cambridge. Ramanujan apparently had now accepted the proposal; as Neville put it, "Ramanujan needed no converting and that his parents' opposition had been withdrawn".[60] Apparently, Ramanujan's mother had a vivid dream in which the family Goddess Namagiri commanded her "to stand no longer between her son and the fulfilment of his life's purpose".[60]
[edit] Life in England
Ramanujan boarded the S.S. Nevasa on 17 March 1914, and at 10 o'clock in the morning, the ship departed from Madras.[71] He arrived in London on 14 April, with E. H. Neville waiting for him with a car. Four days later, Neville took him to his house on Chesterton Road in Cambridge. Ramanujan immediately began his work with Littlewood and Hardy. After six weeks, Ramanujan moved out of Neville's house and took up residence on Whewell's Court, just a five-minute walk from Hardy's room.[72] Hardy and Ramanujan began to take a look at Ramanujan's notebooks. Hardy had already received 120 theorems from Ramanujan in the first two letters, but there were many more results and theorems to be found in the notebooks. Hardy saw that some were wrong, others had already been discovered, while the rest were new breakthroughs.[73] Ramanujan left a deep impression on Hardy and Littlewood. Littlewood commented, "I can believe that he's at least a Jacobi",[74] while Hardy said he "can compare him only with [Leonhard] Euler or Jacobi."[75]Ramanujan spent nearly five years in Cambridge collaborating with Hardy and Littlewood and published a part of his findings there. Hardy and Ramanujan had highly contrasting personalities. Their collaboration was a clash of different cultures, beliefs and working styles. Hardy was an atheist and an apostle of proof and mathematical rigour, whereas Ramanujan was a deeply religious man and relied very strongly on his intuition. While in England, Hardy tried his best to fill the gaps in Ramanujan's education without interrupting his spell of inspiration.
Ramanujan was awarded a B.A. degree by research (this degree was later renamed PhD) in March 1916 for his work on highly composite numbers, which was published as a paper in the Journal of the London Mathematical Society. The paper was over 50 pages with different properties of such numbers proven. Hardy remarked that this was one of the most unusual papers seen in mathematical research at that time and that Ramanujan showed extraordinary ingenuity in handling it. On 6 December 1917, he was elected to the London Mathematical Society. He became a Fellow of the Royal Society in 1918, becoming the second Indian to do so, following Ardaseer Cursetjee in 1841, and he was one of the youngest Fellows in the history of the Royal Society. He was elected "for his investigation in Elliptic functions and the Theory of Numbers." On 13 October 1918, he became the first Indian to be elected a Fellow of Trinity College, Cambridge.[76]
[edit] Illness and return to India
Plagued by health problems throughout his life, living in a country far away from home, and obsessively involved with his mathematics, Ramanujan's health worsened in England, perhaps exacerbated by stress and by the scarcity of vegetarian food during the First World War. He was diagnosed with tuberculosis and a severe vitamin deficiency and was confined to a sanatorium.Ramanujan returned to Kumbakonam, India in 1919 and died soon thereafter at the age of 32. His widow, S. Janaki Ammal, lived in Chennai (formerly Madras) until her death in 1994.[77]
A 1994 analysis of Ramanujan's medical records and symptoms by Dr. D.A.B. Young concluded that it was much more likely he had hepatic amoebiasis, a parasitic infection of the liver widespread in Madras, where Ramanujan had spent time. He had two episodes of dysentery before he left India. When not properly treated dysentery can lie dormant for years and lead to hepatic amoebiasis,[3] a difficult disease to diagnose, but once diagnosed readily cured.[3]
[edit] Personality and spiritual life
Ramanujan has been described as a person with a somewhat shy and quiet disposition, a dignified man with pleasant manners.[78] He lived a rather Spartan life while at Cambridge. Ramanujan's first Indian biographers describe him as rigorously orthodox. Ramanujan credited his acumen to his family Goddess, Namagiri of Namakkal. He looked to her for inspiration in his work,[79] and claimed to dream of blood drops that symbolised her male consort, Narasimha, after which he would receive visions of scrolls of complex mathematical content unfolding before his eyes.[80] He often said, "An equation for me has no meaning, unless it represents a thought of God."[81][82]Hardy cites Ramanujan as remarking that all religions seemed equally true to him.[83] Hardy further argued that Ramanujan's religiousness had been romanticised by Westerners and overstated—in reference to his belief, not practice—by Indian biographers. At the same time, he remarked on Ramanujan's strict observance of vegetarianism.
[edit] Mathematical achievements
In mathematics, there is a distinction between having an insight and having a proof. Ramanujan's talent suggested a plethora of formulae that could then be investigated in depth later. It is said that Ramanujan's discoveries are unusually rich and that there is often more to them than initially meets the eye. As a by-product, new directions of research were opened up. Examples of the most interesting of these formulae include the intriguing infinite series for π, one of which is given below for π, which is correct to six decimal places.
for π, which is correct to six decimal places.One of his remarkable capabilities was the rapid solution for problems. He was sharing a room with P. C. Mahalanobis who had a problem, "Imagine that you are on a street with houses marked 1 through n. There is a house in between (x) such that the sum of the house numbers to left of it equals the sum of the house numbers to its right. If n is between 50 and 500, what are n and x?" This is a bivariate problem with multiple solutions. Ramanujan thought about it and gave the answer with a twist: He gave a continued fraction. The unusual part was that it was the solution to the whole class of problems. Mahalanobis was astounded and asked how he did it. "It is simple. The minute I heard the problem, I knew that the answer was a continued fraction. Which continued fraction, I asked myself. Then the answer came to my mind", Ramanujan replied.[84][85]
His intuition also led him to derive some previously unknown identities, such as
In 1918, Hardy and Ramanujan studied the partition function P(n) extensively and gave a non-convergent asymptotic series that permits exact computation of the number of partitions of an integer. Hans Rademacher, in 1937, was able to refine their formula to find an exact convergent series solution to this problem. Ramanujan and Hardy's work in this area gave rise to a powerful new method for finding asymptotic formulae, called the circle method.[86]
He discovered mock theta functions in the last year of his life. For many years these functions were a mystery, but they are now known to be the holomorphic parts of harmonic weak Maass forms.
[edit] The Ramanujan conjecture
Main article: Ramanujan–Petersson conjecture
Although there are numerous statements that could bear the name Ramanujan conjecture,
there is one statement that was very influential on later work. In
particular, the connection of this conjecture with conjectures of André Weil in algebraic geometry opened up new areas of research. That Ramanujan conjecture is an assertion on the size of the tau function, which has as generating function the discriminant modular form Δ(q), a typical cusp form in the theory of modular forms. It was finally proven in 1973, as a consequence of Pierre Deligne's proof of the Weil conjectures. The reduction step involved is complicated. Deligne won a Fields Medal in 1978 for his work on Weil conjectures.[87][edit] Ramanujan's notebooks
Further information: Ramanujan's lost notebook
While still in India, Ramanujan recorded the bulk of his results in four notebooks of loose leaf
paper. These results were mostly written up without any derivations.
This is probably the origin of the misperception that Ramanujan was
unable to prove his results and simply thought up the final result
directly. Mathematician Bruce C. Berndt,
in his review of these notebooks and Ramanujan's work, says that
Ramanujan most certainly was able to make the proofs of most of his
results, but chose not to.This style of working may have been for several reasons. Since paper was very expensive, Ramanujan would do most of his work and perhaps his proofs on slate, and then transfer just the results to paper. Using a slate was common for mathematics students in India at the time. He was also quite likely to have been influenced by the style of G. S. Carr's book, which stated results without proofs. Finally, it is possible that Ramanujan considered his workings to be for his personal interest alone; and therefore only recorded the results.[88]
The first notebook has 351 pages with 16 somewhat organized chapters and some unorganized material. The second notebook has 256 pages in 21 chapters and 100 unorganised pages, with the third notebook containing 33 unorganised pages. The results in his notebooks inspired numerous papers by later mathematicians trying to prove what he had found. Hardy himself created papers exploring material from Ramanujan's work as did G. N. Watson, B. M. Wilson, and Bruce Berndt.[88] A fourth notebook with 87 unorganised pages, the so-called "lost notebook", was rediscovered in 1976 by George Andrews.[3]
[edit] Ramanujan–Hardy number 1729
Main article: 1729 (number)
A common anecdote about Ramanujan relates to the number 1729. Hardy
arrived at Ramanujan's residence in a cab numbered 1729. Hardy commented
that the number 1729 seemed to be uninteresting. Ramanujan is said to
have stated on the spot that it was actually a very interesting number
mathematically, being the smallest natural number representable in two
different ways as a sum of two cubes:[edit] Other mathematicians' views of Ramanujan
Hardy said : "The limitations of his knowledge were as startling as its profundity. Here was a man who could work out modular equations and theorems... to orders unheard of, whose mastery of continued fractions was... beyond that of any mathematician in the world, who had found for himself the functional equation of the zeta function and the dominant terms of many of the most famous problems in the analytic theory of numbers; and yet he had never heard of a doubly periodic function or of Cauchy's theorem, and had indeed but the vaguest idea of what a function of a complex variable was...".[89] When asked about the methods employed by Ramanujan to arrive at his solutions, Hardy said that they were "arrived at by a process of mingled argument, intuition, and induction, of which he was entirely unable to give any coherent account."[90] He also stated that he had "never met his equal, and can compare him only with Euler or Jacobi."[90]Quoting K. Srinivasa Rao,[91] "As for his place in the world of Mathematics, we quote Bruce C. Berndt: 'Paul Erdős has passed on to us Hardy's personal ratings of mathematicians. Suppose that we rate mathematicians on the basis of pure talent on a scale from 0 to 100, Hardy gave himself a score of 25, J.E. Littlewood 30, David Hilbert 80 and Ramanujan 100.'"
In his book Scientific Edge, noted physicist Jayant Narlikar spoke of "Srinivasa Ramanujan, discovered by the Cambridge mathematician Hardy, whose great mathematical findings were beginning to be appreciated from 1915 to 1919. His achievements were to be fully understood much later, well after his untimely death in 1920. For example, his work on the highly composite numbers (numbers with a large number of factors) started a whole new line of investigations in the theory of such numbers."
During his lifelong mission in educating and propagating mathematics among the school children in India, Nigeria and elsewhere, P.K. Srinivasan has continually introduced Ramanujan's mathematical works.
[edit] Recognition
Ramanujan's home state of Tamil Nadu celebrates 22 December (Ramanujan's birthday) as 'State IT Day', memorializing both the man and his achievements, as a native of Tamil Nadu. A stamp picturing Ramanujan was released by the Government of India in 1962 – the 75th anniversary of Ramanujan's birth – commemorating his achievements in the field of number theory.Since the Centennial year of Srinivasa Ramanujan,every year 22 Dec, is celebrated as Ramanujan Day by the Government Arts College, Kumbakonam where he had studied and later dropped out. It is celebrated by the Department Of Mathematics by organising one-, two-, or three-day seminar by inviting eminent scholars from universities/colleges, and participants are mainly students of Mathematics, research scholars, and professors from local colleges. It has been planned to celebrate the 125-th birthday in a grand manner by inviting the foreign Eminent Mathematical scholars of this century viz., G E Andrews. and Bruce C Berndt, who are very familiar with the contributions and works of Ramanujan.
Every year, in Chennai (formerly Madras), the Indian Institute of Technology (IIT), Ramanujan's work and life are celebrated on 22 December. The Department of Mathematics celebrates this day by organising a National Symposium On Mathematical Methods and Applications (NSMMA) for one day by inviting Eminent scholars from India and foreign countries.
A prize for young mathematicians from developing countries has been created in the name of Ramanujan by the International Centre for Theoretical Physics (ICTP), in cooperation with the International Mathematical Union, who nominate members of the prize committee. The Shanmugha Arts, Science, Technology & Research Academy (SASTRA), based in the state of Tamil Nadu in South India, has instituted the SASTRA Ramanujan Prize of $10,000 to be given annually to a mathematician not exceeding the age of 32 for outstanding contributions in an area of mathematics influenced by Ramanujan. The age limit refers to the years Ramanujan lived, having nevertheless still achieved many accomplishments. This prize has been awarded annually since 2005, at an international conference conducted by SASTRA in Kumbakonam, Ramanujan's hometown, around Ramanujan's birthday, 22 December.
[edit] In popular culture
- An international feature film on Ramanujan's life was announced in 2006 as due to begin shooting in 2007. It was to be shot in Tamil Nadu state and Cambridge and be produced by an Indo-British collaboration and co-directed by Stephen Fry and Dev Benegal.[92] A play, First Class Man by Alter Ego Productions,[93] was based on David Freeman's First Class Man. The play is centred around Ramanujan and his complex and dysfunctional relationship with Hardy.
- Another film, based on the book The Man Who Knew Infinity: A Life of the Genius Ramanujan by Robert Kanigel, is being made by Edward Pressman and Matthew Brown.[94]
- In the film Good Will Hunting, the eponymous character is compared to Ramanujan.
- "Gomez", a short story by Cyril Kornbluth, describes the conflicted life of an untutored mathematical genius, clearly based on Ramanujan.
- A Disappearing Number is a recent British stage production by the company Complicite that explores the relationship between Hardy and Ramanujan.
- The character Amita Ramanujan on the television show Numb3rs is named after Ramanujan.
- The novel The Indian Clerk by David Leavitt explores in fiction the events following Ramanujan's letter to Hardy.[95][96]
- On 22 March 1988, the PBS Series Nova aired a documentary about Ramanujan, "The Man Who Loved Numbers" (Season 15, Episode 9).[97]
- On 16 October 2011 it is announced that Roger Spottiswoode, best known for his James Bond film Tomorrow Never Dies, is working on a movie on mathematical genius Srinivasa Ramanujan starring Rang De Basanti actor Siddharth. Titled The First Class Man, the film's scripting has been completed and shooting is being planned from 2012.[98]
গণিত অলিম্পিয়াডের তথ্য ও প্রশ্ন দেখতে ভিজিট করুন :
http://www.matholympiad.org.bd


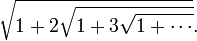
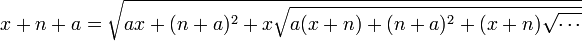





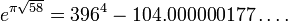
![\left [ 1+2\sum_{n=1}^\infty \frac{\cos(n\theta)}{\cosh(n\pi)} \right ]^{-2} + \left [1+2\sum_{n=1}^\infty \frac{\cosh(n\theta)}{\cosh(n\pi)} \right ]^{-2} = \frac {2 \Gamma^4 \left ( \frac{3}{4} \right )}{\pi}](http://upload.wikimedia.org/wikipedia/en/math/9/9/5/995e72431ce1120e550f2972eb366665.png)

